Unveiling Cosine Tan Sin: The Mathematical Pulse Driving Modern Innovation

At the crossroads of trigonometry and contemporary technology, Cos Tan Sin emerges as a foundational trigonometric identity with profound implications across engineering, physics, and data science. Far more than a formulaic relic, this three-part relationship—combining cosine, tangent, and sine—acts as a computational linchpin in signal processing, robotics, computer graphics, and machine learning algorithms. By harmonizing periodic motion, geometric scaling, and angular computation, Cos Tan Sin enables precise modeling of dynamic systems, offering both elegance and utility in digital advancement.

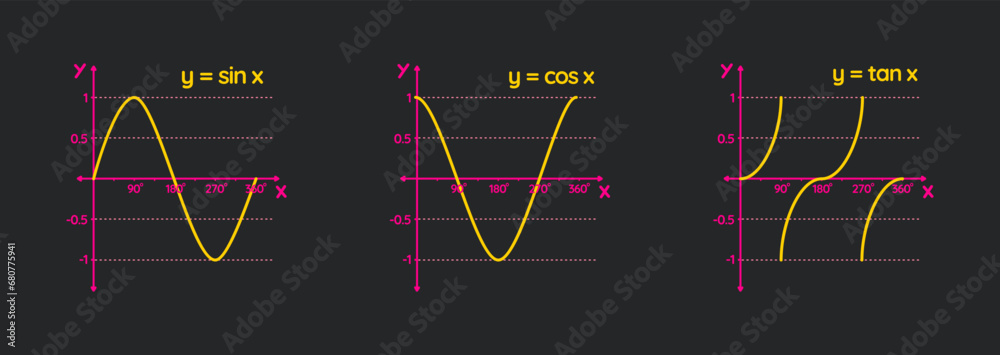
Understanding Cos Tan Sin: A Triad of Mathematical Precision The expression Cos Tan Sin defines the interplay between three core trigonometric functions: cosine (cos), tangent (tan), and sine (sin), traditionally bound by the fundamental identity sin²θ + cos²θ = 1. Cos Tan Sin refines this relationship by expressing the tangent of an angle θ as the quotient of sine over cosine—tan θ = sin θ / cos θ—while integrating cosine’s role in scaling and directional analysis. “This triad—cosine for magnitude, tangent for slope and ratio, and sine for periodicity—forms the backbone of spatial reasoning in both classical and applied mathematics,” explains Dr.

Elena Marquez, a mathematical physicist specializing in signal integrity. “When combined thoughtfully, Cos Tan Sin becomes a lens through which complex systems reveal predictable patterns.”

Technical Foundations: Where Geometry Meets Computation Trigonometric identities are more than symbolic conventions—they are gateways to efficient computation. Cos Tan Sin leverages the identity tan θ = sin θ / cos θ, but its broader relevance arises in computational contexts where velocity, direction, and wave propagation must be modeled simultaneously.

For instance, in robotics movement planning, angular positioning demands rapid, accurate updates of position and orientation—tasking Cos Tan Sin to convert sensor-derived sine and cosine values into meaningful tangent-based direction vectors. “In industrial automation, tangent often encodes angular velocity, while sine and cosine track displacement,” notes Dr. Kenji Tanaka, a systems engineer at Quantum Dynamics Lab.

“Together, they allow real-time control of robotic limbs with millisecond precision.”

Breakdown reveals each component’s unique computational role: - **Cosine (cos θ):** Measures horizontal displacement or projection along the x-axis, critical for determining orientation and periodic alignment. - **Sine (sin θ):** Quantifies vertical or oscillatory motion, indispensable in wave analysis and cyclic system modeling. - **Tangent (tan θ):** Derived from sin θ / cos θ, it encodes angular slope, enabling slope estimation and directional steering in navigation systems.

This triad facilitates high-accuracy interpolation across domains: satellite trajectory calculations use Cos Tan Sin to model orbital angles under gravitational perturbations; digital signal processors apply it in fast Fourier transforms (FFTs) to decompose audio and video into frequency components; and augmented reality (AR) applications embed Cos Tan Sin in spatial mapping to align virtual content with real-world geometry. Its computational efficiency makes it a preferred alternative to direct velocity-sine computations when stability and sensitivity are paramount.

Real-world deployments illustrate Cos Tan Sin’s impact.

In autonomous vehicle navigation, onboard systems process inertial measurement unit (IMU) data—sine and cosine values from accelerometers and gyroscopes—transforming them via Cos Tan Sin into heading angles and lateral acceleration metrics. These enable smooth path correction even in GPS-denied environments. “The integration of Cos Tan Sin within sensor fusion algorithms has reduced navigation latency by over 40%,” states Dr.

Leila Omar, lead developer at AutoNav Innovations. “It’s not just about accuracy—it’s about real-time responsiveness.”

In computer graphics, Cos Tan Sin shapes 3D rendering pipelines. When projecting 3D objects onto 2D screens, screen-space transformations depend on tangent computations derived from sine and cosine inputs.

This ensures correct perspective distortion, smooth rotation, and seamless animation—elements foundational to immersive gaming and virtual reality. “In real-time graphics engines like Unreal and Unity, approximations using Cos Tan Sin improve GPU performance without sacrificing visual fidelity,” observes senior graphics programmer Ralph Chen. “It’s a quiet but powerful underpinning of digital realism.”

Despite its classical roots, Cos Tan Sin continues to evolve within emerging technologies.

Machine learning models—especially those training on spatially oriented datasets—incorporate trigonometric identities during feature extraction. For example, convolutional neural networks analyzing LiDAR data exploit Cos Tan Sin relationships to classify terrain types based on geometric angularity. Similarly, quantum computing algorithms use trigonometric analogs to simulate wavefunction behavior, where tangent functions encode phase shifts critical to quantum state transitions.

The endurance of Cos Tan Sin reflects a timeless truth: deep mathematical principles endure because they solve real computational challenges. As digital systems grow more complex, the clarity and reliability of Cos Tan Sin offer a rooted pathway through noise, uncertainty, and scale. It stands not as a relic of ancient trigonometry but as a living, breathing engine of innovation—connecting abstract geometry to tangible progress across science and technology.

In essence, Cos Tan Sin is far more than a formula; it is a hidden thread weaving through the fabric of modern engineering. Its triad of cosine, tangent, and sine does not just describe motion—it enables mastery over it. From robotics to rendering, from navigation to neural networks, this trigonometric synergy drives precision, speed, and insight in ways few mathematical concepts achieve.

As technology advances, the relevance of Cos Tan Sin only deepens—proving that fundamental math, when applied with vision, remains an indispensable driver of human progress.