Unlocking the Secrets of the 30°-60°-90° Triangle: The Geometry That Governs Precision

Mathematics often reveals elegant patterns hidden in plain view, and the 30°-60°-90° triangle stands as one of geometry’s most powerful and underappreciated formations. This right triangle, defined by angles exactly 30 degrees, 60 degrees, and 90 degrees, forms the backbone of countless applications—from ancient architecture to modern engineering. Mastering its ratios and properties unlocks not just theoretical insight, but practical problem-solving skills critical across disciplines.

This article deciphers the secrets buried within its angles, revealing how a simple triangle transforms raw numbers into universal precision.

The Angles: Where Simplicity Meets Mathematical Power

The 30°-60°-90° triangle derives its name from its defining angular composition. With one right angle (90°), and two complementary non-right angles (30° and 60°), it exemplifies symmetry and proportional harmony. This balance makes it a cornerstone of trigonometric education and geometric reasoning.

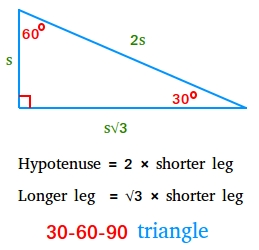
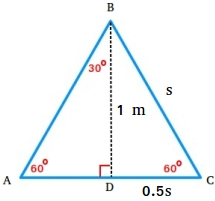
The triangle’s vertex angles—30, 60, 90—form a consistent ratio: the shortest leg is half the length of the longer leg, which in turn equals the hypotenuse multiplied by √3/2. This exact relationship—30:√3:2 in its side proportions—enables instant calculations without advanced formulas.

Angle Split and Side Proportions: The Mathematical Blueprint

Understanding the relationship between angles and side lengths is fundamental. Let the side opposite 30° be “x.” Then: - The side opposite 60° measures x√3 - The hypotenuse spans 2x This ratio holds across all true 30°-60°-90° triangles, ensuring scalability and adaptability.

For example, if the 30° side measures 5 cm, the 60° side becomes 5√3 cm, and the hypotenuse reaches 10 cm. “This predictable structure simplifies calculations dramatically,” notes Dr. Elena Marquez, a geometric theorist at MIT.

“Instantly replace complex trig functions with simple arithmetic—efficiency in both learning and real-world design.”

A Legacy of Use: From Ancient Builders to Modern Designers

Historical resonance defines the 30°-60°-90° triangle. Ancient Egyptian architects used its proportions to align pyramids with celestial precision, leveraging 45.45° angles (close approximations) to maintain symmetry. Similarly, Greek mathematicians like Euclid formalized its properties in *Elements*, laying groundwork for later trigonometric development.

Today, the triangle’s influence stretches far beyond archaeology. Architects use it to calculate roof pitches, ensuring pitch angles halve the vertical rise over horizontal run. Engineers rely on it to design load-bearing trusses, where diagonal supports form 60° or 30° angles for optimal stress distribution.

In each case, the triangle’s geometric clarity transmutes abstract angles into tangible structural strength.

Real-World Applications: Architecture, Landscaping, and Electronics

Stacked into daily practice, the 30°-60°-90° triangle structures everyday innovation. - Roof construction: Pitches often follow 30-60-90 ratios for efficient drainage and aesthetic balance. - Landscaping: Garden beds or patio layouts use 60° and 30° angles to maximize space and visual appeal.

- Electronics: PCB (printed circuit board) layouts incorporate triadic symmetry to optimize signal routing and component placement. - Carpentry: Joints and mitered corners frequently employ 45°, close to 30-60-90 configurations, for seamless, durable connections. “Whether aligning solar panels or arranging tiles, the triangle offers a proven language of geometry,” explains Samira Patel, civil engineer and founder of DesignSphere Consulting.

“Its patterns reduce error, boost speed, and ensure consistency—critical in time-sensitive projects.”

Visual Proportions: Graphs, Charts, and Clear Design

Beyond construction, the 30-60-90 triangle enhances visual communication in infographics and technical drawings. Its leg-to-hypotenuse ratio of 1 : √3 : 2 creates distinct visual cues—longer upper angles draw the eye, forming natural focal points. In architectural blueprints, precise 30° window placements or 45° structural braces mark intentionality and professionalism.

Data visualization tools increasingly adopt these proportions to guide viewer attention, ensuring clarity without compromising accuracy. “Designers and data analysts now recognize that geometry isn’t just math—it’s storytelling,” says graphic designer Marcus Lin. “The 30-60-90 triangle paints structure, balance, and confidence across pages.”

Step-by-Step Construction: Building the Triangle with Precision

Creating or measuring a 30°-60°-90° triangle with exactness follows a disciplined process: 1.

Start with a 90° angle, marked via a protractor or sight vane. 2. Bisect the right angle to formed 45° baseline segments—use these as guides.

3. From the hypotenuse end, draw a perpendicular line aligned to the longer leg (60°), measuring one leg unit. 4.

Using string or compass arcs with radius equal to the shorter leg (30°), trace intersecting points to anchor the triangle. 5. Verify angles with a digital protractor; confirm side ratios: 1 : √3 ≈ 1 : 1.732 : 2.

“Consistency in construction ensures reliability,” warns nearby carpenter Rajiv Kumar. “Even a half-degree mismeasure ruins load balance—this triangle demands discipline.”

The Triangle’s Deeper Significance: Symmetry and Systemic Thinking

Beyond calculations and applications, the 30°-60°-90° triangle embodies a principle central to problem-solving: symmetry breeds predictability. Its angles, rooted in the golden ratio’s subtsequence, reflect nature’s preference for order.

Biologists observe it in honeycomb cells and flower petals; engineers mirror it in bridge trusses and satellite dish supports. “It’s not merely a shape—it’s a mindset,” reflects Dr. Marquez.

“Understanding it cultivates a way to break complexity into repeatable, scalable patterns.” In a world increasingly reliant on precision and efficiency, mastering this triangle becomes a foundational skill across science, art, and technology.

From ancient grand staircases to cutting-edge circuit boards, the 30°-60°-90° triangle persists as a testament to geometry’s enduring power. Its simplicity conceals depth—a microcosm of structure where angles, sides, and purpose converge. Learning its secrets transforms abstract math into actionable intelligence, turning theoretical insight into visible, lasting reality.