The Tan Half-Angle: A Foundational Tool in Trigonometry and Beyond
The Tan Half-Angle: A Foundational Tool in Trigonometry and Beyond
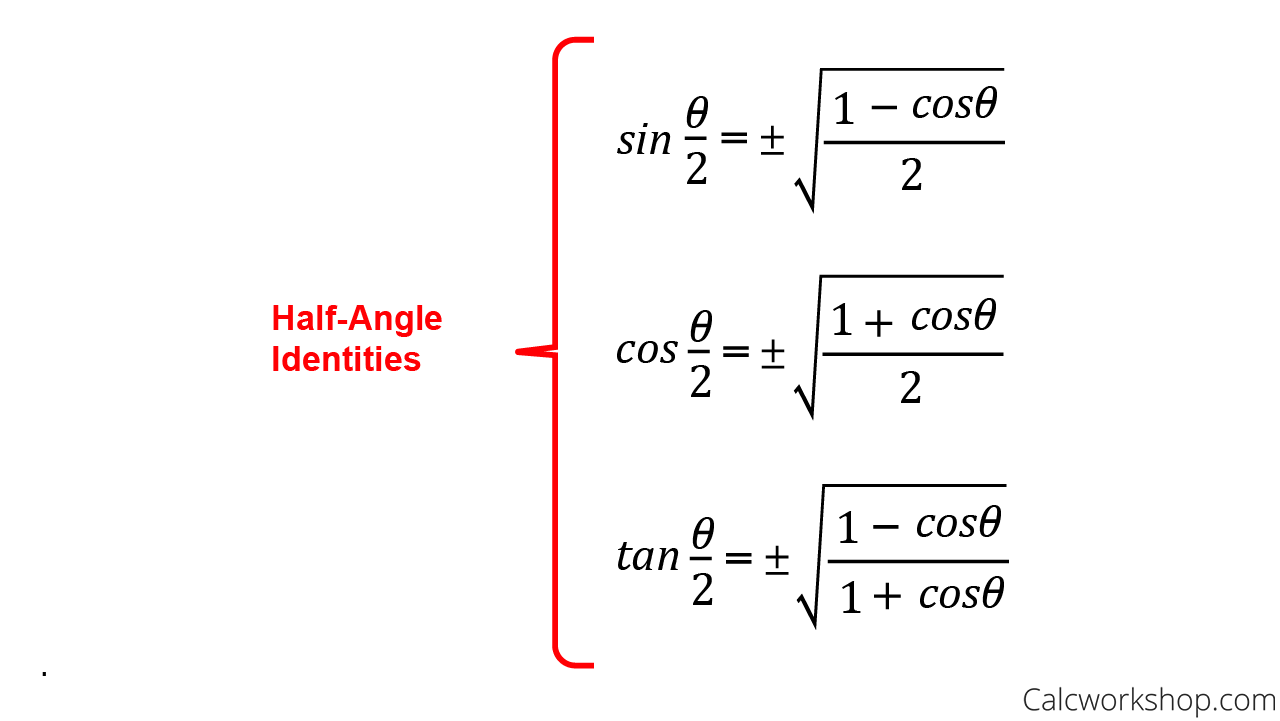
In the intricate world of advanced trigonometry, few tools are as underappreciated yet profoundly useful as the tan half-angle substitution. This elegant identity—often expressed as tan(θ/2) = (1 − cos θ) / sin θ or equivalently tan(θ/2) = sin θ / (1 + cos θ)—transforms complex angular calculations into simpler, solvable forms. Rooted in ancient mathematical traditions and indispensable in modern engineering, physics, and geometrical modeling, the tan half-angle remains a cornerstone of analytical precision.
Its power lies not just in substitution, but in unlocking symmetries and simplifying integrations that would otherwise demand elaborate computation.
At its core, the tan half-angle formula arises from the interplay between sine and cosine identities, leveraging the tangent’s unique ability to express ratios regardless of quadrant. The standard substitution—tan(θ/2) = t—serves as a bridge, translating trigonometric expressions involving double angles or periodic functions into linear equations in t. This transformation enables solutions to otherwise intractable problems across fields ranging from signal processing to structural analysis.
Mathematical Foundations and Derivation
The derivation of the tan half-angle identity begins with fundamental Pythagorean relationships.Starting from the double-angle formula for sine, sin θ = 2 sin(θ/2) cos(θ/2), and dividing both sides by cos²(θ/2), one navigates through identities to obtain tan(θ/2). Using sin θ = 2t / (1 + t²) and cos θ = (1 − t²) / (1 + t²), where t = tan(θ/2), substitution yields the canonical form.
“The half-angle substitution turns circular complexity into linear simplicity, enabling analytic mastery over otherwise unwieldy expressions.”This algebraic pathway confirms tan(θ/2) as a rational function of sin θ and cos θ, defined for all θ except odd multiples of π where cos(θ/2) vanishes.
Its invertibility across quadrants enhances utility in parametric equations and cyclical systems.
Applications in Engineering and Physics
In electrical engineering, the tan half-angle formula plays a crucial role in analyzing phase shifts and waveform modulation. When evaluating alternating current (AC) circuits, phase difference between voltage and current often involves half-angle identities.For instance, in a series RLC circuit, the impedance ratio depends on tan(ωt/2), where ω is angular frequency and t is time. Simplifying such expressions accelerates the design and stability analysis of oscillators and filters. In optics and wave propagation, the identity aids in modeling interference patterns and diffraction effects.
By expressing phase contributions through t = tan(φ/2), researchers resolve complex interference conditions into tractable algebraic forms, streamlining both theoretical predictions and experimental calibration.
Civil engineers deploy the tan half-angle technique when calculating intentional slopes—such as road grades or drainage channels—where precise angular gradients dictate safety and efficiency. By substituting tan(θ/2) = (1 − cos θ)/sin θ into slope formulas, designers convert trigonometric constraints into linear stress and flow equations, enabling robust resource allocation and structural integrity checks.
Computer graphics and computational geometry rely heavily on half-angle substitutions for rendering curves and animations.
When computing smooth transitions between angular states—critical in 3D modeling or virtual reality—tan(θ/2) facilitates interpolation between keyframes, ensuring fluid motion without computational spikes. This application underscores its value beyond pure mathematics into the realm of interactive digital design.
Simplification of Integrals and Analytical Calculus
One of the tan half-angle’s most celebrated roles is in integral calculus, where standard trigonometric integrals resist elementary methods. The substitution t = tan(θ/2) converts rational trigonometric integrals—such as ∫ sin x / (1 + cos x) dx—into rational functions of t, opener for partial fraction decomposition and standard integration tables.For example, ∫ sec²(θ/2) dθ reduces immediately to ∫ (1 + t²)/(1 + t²) dt = ∫ dt, yielding a resolution in minutes instead of iterative trial and error. This efficiency extends to advanced calculus, including improper integrals over periodic functions and Fourier series expansions, where periodic symmetry aligns naturally with half-angle parametrization.
Geometric Interpretations and Visual Applications
Beyond algebra and calculus, the tan half-angle governs geometric constructions with surprising elegance.In coordinate transformations, projecting 3D points onto planar or meridian fields often employs t = tan(φ/2), linking elevation angles to linear coordinate shifts. This technique simplifies map projections, aerospace navigation, and robotic arm positioning, where angular precision directly impacts positional accuracy. In computational geometry, midpoint and angular bisectors—critical in Voronoi diagrams and Delaunay triangulations—implicitly depend on tangent half-angle identities.
These structures, foundational in geographic information systems (GIS) and finite element analysis, gain computational stability through substitution-driven refinements.
Educational Impact and Modern Pedagogy
Teaching advanced trigonometry remains a challenge, as students grapple with abstract identities and symbolic manipulation. The tan half-angle, with its computational duality, serves as an ideal pedagogical bridge: it demystifies double-angle formulas by grounding them in linear algebra, reduces integration to algebraic decomposition, and fosters intuition about angular symmetry.Educators increasingly integrate interactive software that visualizes tan(θ/2) transformations—displaying how complex waveforms split into manageable harmonic components. This hands-on approach, supported by computational tools, accelerates comprehension and cultivates mastery, preparing students for careers in data science, physics, and engineering.
Limitations and Practical Considerations
While powerful, the tan half-angle demands careful handling.Its definition excludes θ = π + 2πn where cos(θ/2) = 0, risking division by zero. Additionally, domain restrictions require verification when translating real-world problems into mathematical models. Within its defined scope, however, its utility far exceeds constrained drawbacks.
Moreover, numerical stability must be monitored in floating-point computations—small errors in tan(θ/2) can propagate in iterative algorithms. Rigorous software implementation, including edge-case validation, ensures reliable outcomes across scientific and engineering applications.
The Enduring Legacy of Tan Half-Angle Thinking
From ancient astronomers calculating celestial paths to modern engineers optimizing 5G signal arrays, the tan half-angle remains an indispensable tool.Its transformation of complex angular relationships into linear frameworks exemplifies how mathematical innovation enables practical breakthroughs. Far more than a formula, it embodies a mindset—one that sees hidden symmetries, simplifies chaos, and

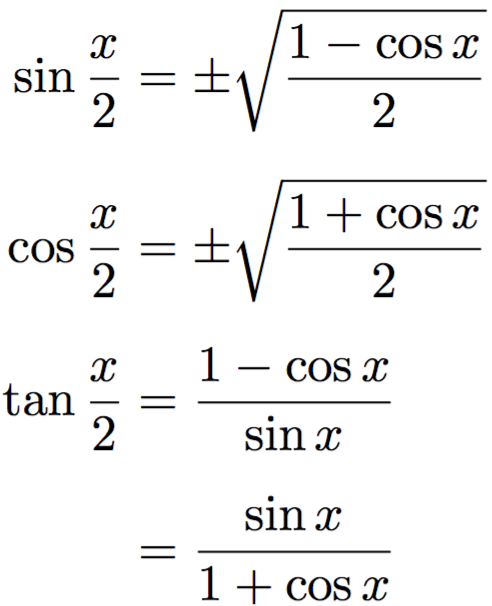

Related Post

Unlocking Trigonometric Secrets: How the Tan Half Angle Formula Transforms Calculations

Zipcode Of Jacksonville Florida

Honduras vs El Salvador: The Football Rivalry That Rages Across Borders and Hearts

What Is Level D in Irey Math? Decoding the Key Stage for Success

