Master the Math: The Essential Degrees to Radians Conversion Guide

Understanding angular measurements is foundational to fields ranging from engineering and physics to computer graphics and robotics—but few subjects spark more head-scratching confusion than converting degrees to radians. While degrees dominate common coordinate systems and angular descriptions, radians serve as the natural unit in mathematical and scientific calculations, particularly in calculus, physics, and signal processing. This guide demystifies the conversion with a clear, step-by-step approach that empowers readers to transition seamlessly between these two essential angular representations—no jargon, no complexity, just practical clarity.

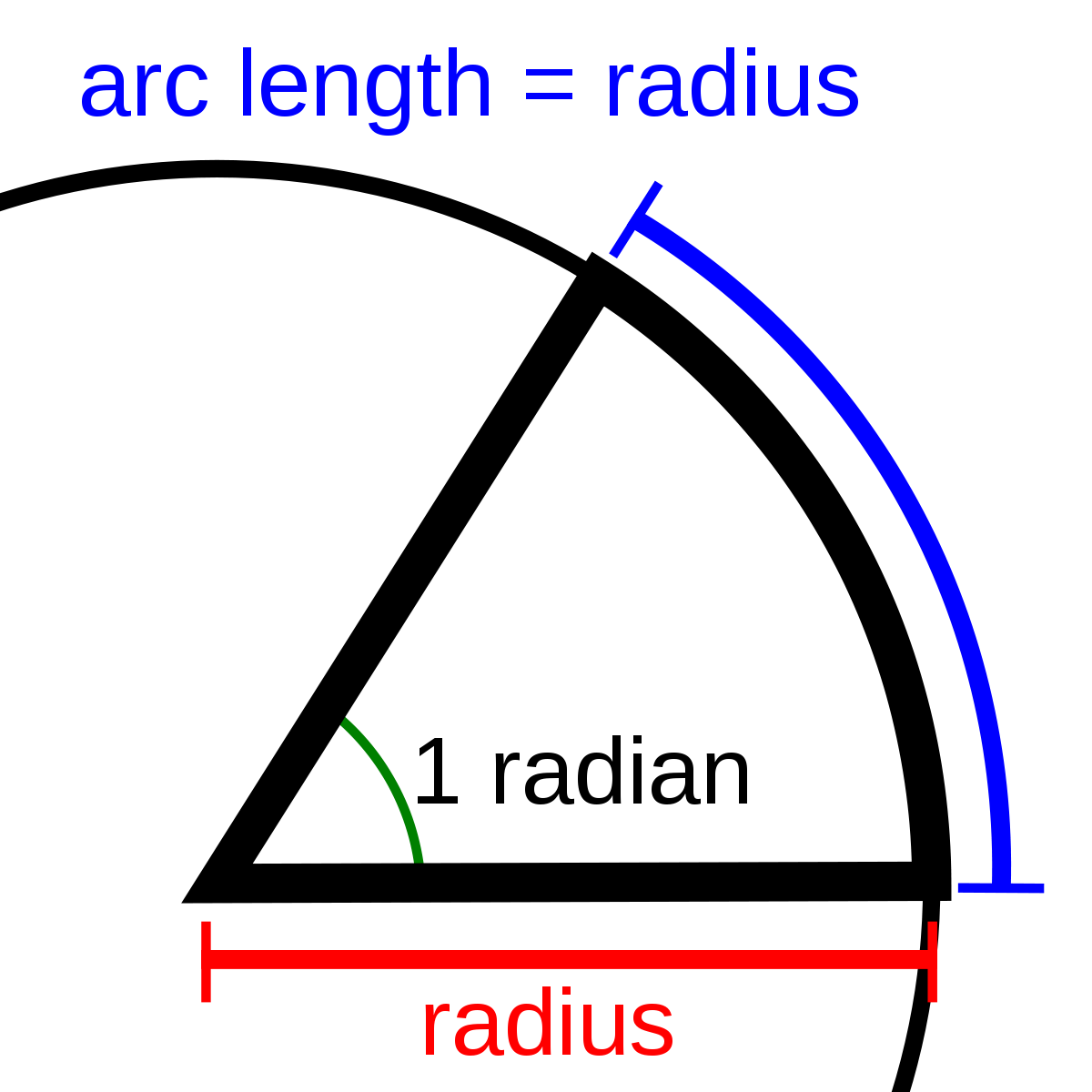
## Why Radians Matter: Beyond Degrees in Technical Fields Radians express angles as a ratio: one radian is the angle subtended at the center of a circle by an arc whose length equals the radius. Unlike degrees, which are arbitrary divisions of a circle into 360 parts, radians provide a dimensionless, mathematically elegant measure. In calculus, derivatives and integrals of trigonometric functions simplify dramatically when angles are expressed in radians.

For instance, the derivative of sine is simply cosine—but only when the input is in radians. > “Radians are the language of motion in mathematics,” says Dr. Elena Torres, applied mathematician at MIT.

“They bridge geometry and physics with precision.” Engineers rely on radians when modeling rotational dynamics, while physicists use them in wave mechanics and quantum theory. Even in computer graphics, where smooth rotational calculations are vital, radians prevent distortion and maintain fidelity across frame updates. ## The Core Formula: Converting Degrees to Radians At first glance, the conversion between degrees and radians appears simple—but only if one remembers the defining relationship.

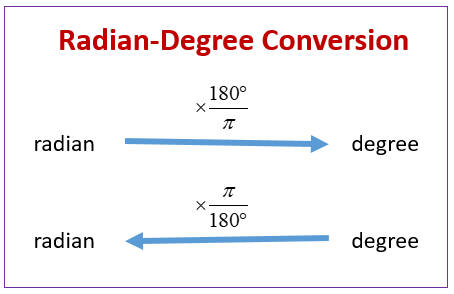
The fundamental formula is: radians = degrees × (π / 180) This equation stems directly from the definition of a radian and the circumference of a circle. Since a full circle measures 360 degrees, and the corresponding arc length equals the radius, the ratio of arc length to radius is π/180 radians. Multiplying degrees by π/180 converts angular measure from arbitrary divisions to this mathematically consistent unit.

This formula is not arbitrary; it’s rooted in the geometry of the circle. For example, 180 degrees equals π radians, which means each degree corresponds to π/180 radians—approximately 0.017453 radians per degree. ## Step-by-Step: How to Convert Degrees to Radians Clearly To convert any angle from degrees to radians, apply the formula methodically: first convert degrees into a fractional form (often un-needed, since it's multiplied directly by π/180), then apply the multiplication.

No need for prior angle normalization—degrees naturally integrate into the equation. - Start with the degree value (e.g., 45°, 120°, or even 270°). - Multiply by π (pi ≈ 3.1416), then divide by 180.

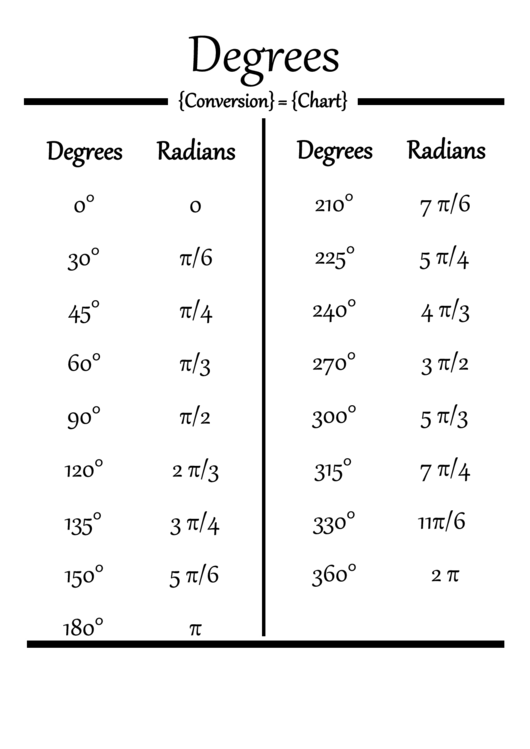
- The result is the angle in radians. Formula in practice: radians = (degrees × π) ÷ 180 This direct calculation ensures accuracy, eliminating rounding errors common when using approximate values like 22/7. ## Examples That Clarify: Seeing It in Action Let’s solidify understanding with illustrations: - **45 degrees:** (45 × π) ÷ 180 ≈ (45 × 3.1416) ÷ 180 ≈ 141.372 ÷ 180 ≈ 0.7854 radians - **90 degrees:** (90 × π) ÷ 180 = 90π/180 = π/2 ≈ 1.5708 radians - **180 degrees:** (180 × π) ÷ 180 = π ≈ 3.1416 radians - **360 degrees:** (360 × π) ÷ 180 = 2π ≈