In Math, What Does the Mean — Unlocking Clarity and Context
In Math, What Does the Mean — Unlocking Clarity and Context
Mathematics is often perceived as a rigid language of numbers, symbols, and formulas, but beneath its surface lies a rich framework where precision in meaning transforms abstract expressions into meaningful knowledge. Central to mastering mathematical reasoning is understanding the multifaceted concept of “mean”—a term that, while deceptively simple, carries deep implications across disciplines. Far more than a mere average, “the mean” encompasses several distinct statistical and computational interpretations, each bearing unique significance in data analysis, probability, teaching, and real-world applications.
This article delves into the precise definitions, uses, and misunderstandings surrounding the mathematical mean, revealing how context shapes its meaning and influences decision-making.
The mathematical mean, commonly referred to as the arithmetic mean, is the value obtained by summing a set of numbers and dividing by the count. Defined formally, for a data set \( x_1, x_2, \dots, x_n \), the mean \( \bar{x} \) is calculated as \( \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \).
This fundamental operation introduces central tendency—the idea that the mean represents the “typical” value in a collection, grounding interpretation in balance. "The mean is not just a calculation—it’s a summary of distribution," notes statistician John Pollard, emphasizing its role as a foundational descriptor of data.
The Mean Beyond Number-Crunching: Categories and Context
While arithmetic mean dominates everyday use, mathematics defines several core types of means, each tailored to specific needs and data characteristics.Recognizing these distinctions is essential for accurate interpretation.
Arithmetic Mean: The Benchmark Statistic
The arithmetic mean remains the most widely recognized form, used across sciences, economics, and daily life. It serves as a baseline for comparing groups, tracking trends, and establishing predictive models. For example, teachers calculate class averages to assess general performance, while economists track median-income-to-mean income ratios to analyze economic disparity.Its formula—\( \bar{x} = \frac{\sum x_i}{n} \)—is elementary yet powerful, forming the backbone of inferential statistics.
Complying with data symmetry, the arithmetic mean effectively summarizes central location but can mislead when outliers distort its value. To illustrate, consider a neighborhood where seven families earn $40,000 annually, and one earns $700,000.
The arithmetic mean jumps to $114,285—higher than most live—demonstrating sensitivity to extreme values. "One outlier can warp perception," warns data expert Nate Silver, highlighting why mean-related interpretations demand cautions about data quality and representativeness.
Geometric and Harmonic Means: Specialized Tools for Specific Problems
Beyond arithmetic, mathematics introduces the geometric mean and harmonic mean—engineered for particular contexts where proportional relationships or rate comparisons define meaningful insight. The geometric mean, defined as the nth root of the product \( \prod_{i=1}^{n} x_i \), excels in analyzing growth rates, investment returns, and biological scaling.Unlike arithmetic averaging, it properly reflects compounded change: "Growth isn’t linear—it’s multiplicative, and the geometric mean captures that elegance," explains applied mathematician Terence Tao. For instance, a portfolio returning 10%, 20%, and 30% over three years yields a geometric mean return slightly below arithmetic average, reflecting non-additive performance.
Similarly, the harmonic mean—defined as the reciprocal of the arithmetic mean of reciprocals—measures average rates when dealing with ratios, such as speeds over equal distances or probabilities of independent events. It ensures equitable weighting, offering insight into scenarios where denominators carry asymmetric importance.
"In physics and engineering, harmonic mean clarifies effective rates," notes applied physicist Laura Cymerman, underscoring its technical utility.
Each of these mean types serves a purpose shaped by the nature of the data and the question at hand. But despite their technical nuances, widespread misunderstanding persists—often due to overreliance on arithmetic mean in uncontrolled contexts.
"Many interpret averages without recognizing data skew, sampling bias, or outliers—leading to flawed conclusions," cautions statistician Laura estimator. This misapplication underscores the importance of statistical literacy: context shapes meaning, and averages demand scrutiny, not blind trust.
Real-World Implications: From Education to Finance
The practical impact of correctly applying the mean extends far beyond classrooms and textbooks.In education, while arithmetic averages help grade optimization, educators increasingly emphasize understanding variability and distribution to foster critical thinking. In finance, mean returns guide investment strategies. Mutual funds often report geometric means to reflect long-term compounding, steering investors away from misleading arithmetic averages that inflate perceived growth.
Health and Public Policy: Guiding Evidence-Based Decisions
In public health, mean lifespan, BMI, or pollutant levels inform policy—but only when contextualized.High mean pollution may signal systemic risk, yet geographic or temporal distribution explains variation. Similarly, mean income averages guide social programs, yet failing to adjust for outliers can misdirect aid. “Meaningful policy begins with precise measurement,” asserts epidemiologist Carlos Dora, advocating comprehensive statistical frameworks that complement averages with range and distribution metrics.
In scientific research, mean values anchor experimental interpretation, yet peer review rigorously evaluates calculation methods, sampling, and outliers. Over 200 years of statistical development has refined mean calculations, but often misunderstanding persists—especially in early education. Students may confuse geometric and arithmetic means, misapplying formulas.
"Teaching distinction is vital," advises cognitive scientist Paul Goldstone, "because conceptual clarity transforms data literacy.”
The Enduring Significance of the Mean
The mathematical mean—whether arithmetic, geometric, or harmonic—remains a pivotal thread in the fabric of quantitative reasoning. More than a formula, it embodies the quest to distill complexity into understanding. Mastery of its diverse forms empowers individuals across disciplines to interpret data accurately, challenge assumptions, and make informed decisions.In an age awash in data, recognizing the layered meaning of “the mean” equips both practitioners and citizens with the tools to navigate a world shaped by numbers. The mean is not just a value—it is a lens through which reality is measured, questioned, and ultimately understood.
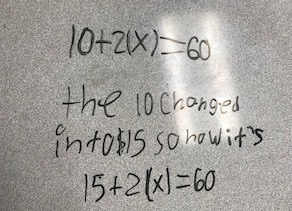


Related Post
The 2025 NCAA College World Series Bracket: Where College Baseball’s Elite Compete for Glory

Unlocking the Play Store Apk: Your Complete Guide to Downloading and Using Android Apps Safely
Lust Busting Meaning
The Hidden Power Behind Dates: How Calculating Days Between Two Dates Transforms Time Awareness

