How Do You Figure Out Acceleration? The Science Behind Speeding Up
How Do You Figure Out Acceleration? The Science Behind Speeding Up
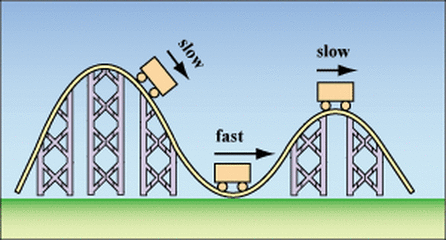
To identify acceleration is not merely a matter of guessing—it’s a precise application of physical principles rooted in observable motion and mathematical modeling. Whether measuring how quickly a car quickens its pace, how rapidly a falling object gathers momentum, or how a sports surge shifts velocity over time, acceleration reveals the hidden rhythm of change. Understanding how to calculate it transforms intuition into actionable knowledge, essential in physics, engineering, sports analytics, and everyday problem-solving.
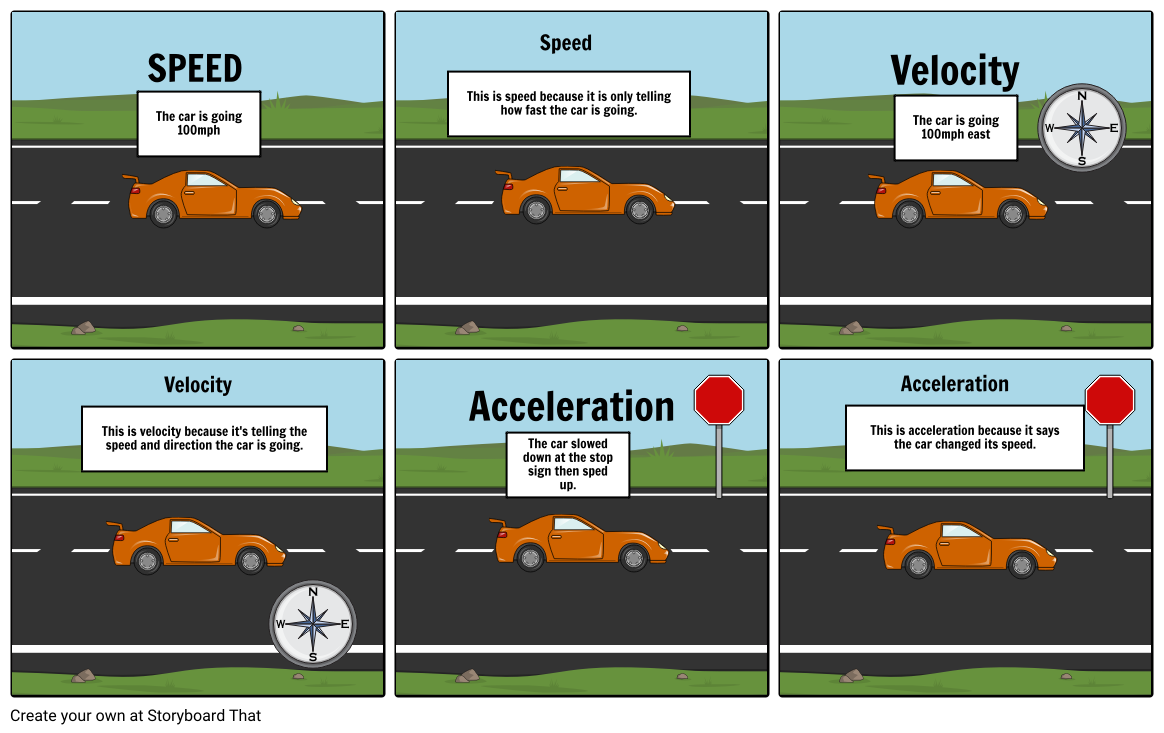
Understanding acceleration begins with its definition: acceleration is the rate at which an object’s velocity changes over time. Mathematically, it is expressed as the change in velocity divided by the time interval during which the change occurs. In formulaic terms:
= (≤ − vi) / (t − ti) where denotes acceleration,
This equation applies across disciplines, from encoding motion in digital simulations to interpreting the trajectory of celestial bodies.
One of the most accessible methods to determine acceleration unfolds in everyday motion tracking: linear velocity measurements. Suppose a vehicle accelerates uniformly along a straight path—say from 10 m/s to 30 m/s in 5 seconds.
By computing the rise in speed divided by the duration, acceleration becomes (30 − 10)/5 = 4 m/s². This straightforward calculation exposes the system’s dynamism, revealing not only speed gain but the force-driven nature of change. But real-world scenarios demand more nuanced approaches, particularly when motion is curved or velocities fluctuate.
For varying or non-uniform motion—such as a thrown ball, a rotating wheel, or a spacecraft adjusting orbit—kinematic equations become indispensable.
These formulas integrate calculus principles, allowing acceleration to be derived from positional data collected over time. For example, acceleration is the second derivative of position with respect to time. If position data is logged in discrete intervals, the average acceleration over a span is calculated as:
≈ (x(t + Δt) − x(t)) / Δt², approximating the instantaneous rate of change from sequential snapshots.
Advanced tools like motion sensors, high-speed cameras, and smartphone accelerometers automate this process, converting empirical data into precise acceleration profiles.
Step-by-Step: Measuring Acceleration in Real-World Scenarios
Here’s how experts determine acceleration across contexts.
- Sports Performance Analytics: In athletics, linear accelerometers embedded in wearable devices capture an athlete’s motion during sprints. Coaches analyze velocity-time graphs, where steep slopes indicate rapid acceleration—critical for optimizing departure speeds in racing or jump height. “Acceleration data reveals the secret to explosive starts—timing bursts with maximal force delivery,” notes Dr.
Elena Ruiz, a biomechanics expert at the National Institute of Sports Science.
- Automotive Engineering:
- Test tracks employ GPS and inertial measurement units (IMUs) to record a vehicle’s velocity and position at millisecond intervals.
- The data feed into software that computes instantaneous acceleration, enabling engineers to refine traction control systems, braking responses, and ride comfort.
- NRC (Newton Research Corporation) models highlight that even fractions of a meter per second squared can affect handling and fuel efficiency.
- Astrophysics and Space Missions:
- Acceleration reveals gravitational influences: spacecraft acceleration tryectories depend on subtle shifts in velocity due to planetary gravity and propulsion.
- By analyzing Doppler radar shifts and onboard sensor logs, mission control deciphers acceleration patterns, ensuring precise orbital insertion and course corrections.
- NASA’s Deep Space Network uses this data to navigate probes through the solar system with extraordinary accuracy.
The Role of Data Precision and Sampling Frequency
While the core formula remains simple, accurate acceleration measurement hinges on precise, high-frequency data. Gaps or low sampling rates introduce noise, skewing results—for example, mistaking a sudden jolt for sustained acceleration. High-resolution IMUs sampling at 100–1000 Hz capture micro-changes vital for detecting anomalies in machinery or optimizing athletic performance.
“Timing errors as small as 10 milliseconds can distort acceleration curves—especially in high-speed events,” warns mechanical engineer Marcus Bell. “You’re not just measuring speed; you’re decoding the physics of change.”
When dealing with theoretical or indirect observations, calculus offers deeper insight. For periodic motion—such as a pendulum or oscillating spring—the instantaneous acceleration at any moment is negative: it always points opposite to the direction of increasing displacement.
This principle underpins Hooke’s Law and harmonic motion models, where acceleration magnitude correlates with velocity squared, enabling engineers to design resilient structures and regulate energy systems efficiently. Equations of motion from Newton’s second law (F = ma) further refine this analysis, linking acceleration directly to net forces.
Common Pitfalls and How to Avoid Them
Misidentifying acceleration often stems from flawed assumptions or measurement errors. For instance, confusing average velocity with acceleration can misrepresent dynamics—a car moving at constant speed exhibits zero acceleration, not steady velocity.
Similarly, neglecting time units (seconds vs. milliseconds) yields nonsensical results (e.g., m/s² instead of m/s), undermining practicality. Consistent calibration of instruments and validation against known reference points—like using identical lab setups or comparative motion traces—help maintain reliability.
In summary, determining acceleration merges measurement science with theoretical rigor, enabling insight into dynamic systems across scales.
From classroom mechanics labs measuring toy car progress to Mars rover navigation guided by microsecond-precise data, accurate acceleration calculation drives progress. It answers critical questions about power, safety, and efficiency—proving that understanding speed change is central to mastering motion itself.
As physics continues advancing, so does the sophistication of acceleration analysis—embedding sensors in vehicles, drones, and even wearable health devices, transforming raw motion into actionable knowledge. Whether optimizing a sprinter’s launch or stabilizing a spacecraft, calculating acceleration remains the silent pulse behind motion’s story.**


Related Post
The Science of Nyt Strands Today: Decoding Daily Answers for Peak Clarity

Is Shark Halal? The Surprising Truth Behind a Controversial Fish

Andrea Henderson: NBC4’s Dynamo – Age, Height, Marriage, and the Life Behind the Mic

Alice Adair: The Brilliant Mind Behind a Pioneering Literary Legacy